第7讲反函数和积分（Inverse Functions & Integration）

💡

一、单射函数与反函数

1.1 单射函数（One-to-One Functions）

设函数 $f$ 的定义域为 $D$ ，若对任意 $a, b ∈ D$ 满足：

a \neq b \Rightarrow f(a) \neq f(b) \\ \text{或等价地} \quad f(a) = f(b) \Rightarrow a = b

则称 $f$ 是单射函数。

学习建议：通过绘制函数图像判断是否通过水平线测试。例如：

$f(x) = x^3$ 是单射函数

$f(x) = \sin x$ 在全体实数上不是单射函数

1.2 反函数定义

设 $f$ 是单射函数，定义域为 $A$ ，值域为 $B$ ，则其反函数 $f^{-1}$ 满足：

定义域 $B$ ，值域 $A$

$f^{-1}(y) = x \iff y = f(x)$

满足 $f^{-1}(f(x)) = x$ 且 $f(f^{-1}(y)) = y$

重要性质：

$(f^{-1})^{-1} = f$

但注意 $(f(x))^{-1} = \frac{1}{f(x)}$ 是倒数而非反函数

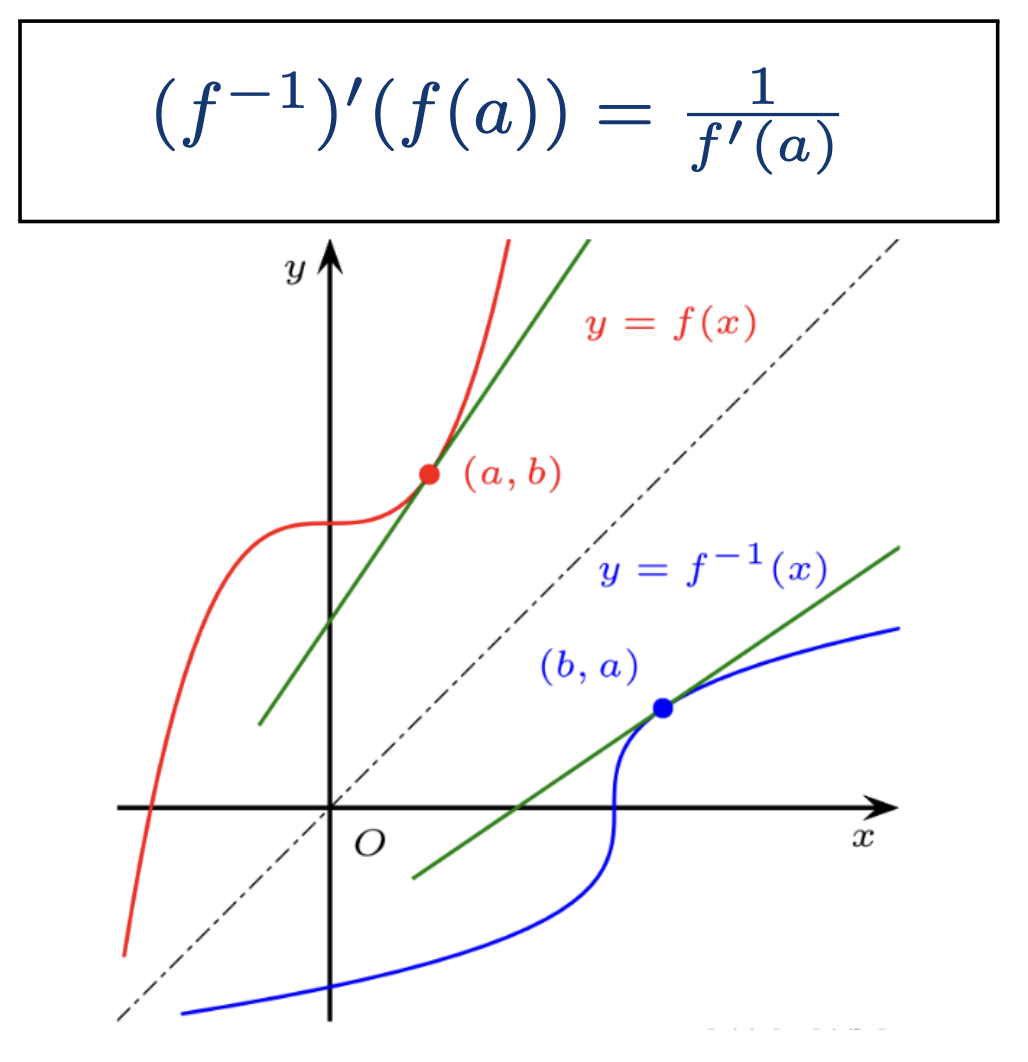
1.3 反函数的导数

若 $f$ 在区间 $I$ 上连续且可导，且 $f'(a) \neq 0$ ，则反函数在 $b = f(a)$ 处可导：

(f^{-1})'(b) = \frac{1}{f'(a)} \\ \text{或等价地} \quad (f^{-1})'(f(a)) = \frac{1}{f'(a)}

例子：设 $f(x) = e^x$ ，则 $f^{-1}(x) = \ln x$

(f^{-1})'(x) = \frac{1}{f'(\ln x)} = \frac{1}{e^{\ln x}} = \frac{1}{x}

二、积分技巧

2.1 有理函数积分

对形如 $\int \frac{A(x)}{B(x)} dx$ 的有理函数：

确保分子次数 < 分母次数（否则先多项式除法）

分解为部分分式：
- 线性因子 $(x+a)^k$ ： $\frac{A_1}{x+a} + \frac{A_2}{(x+a)^2} + \cdots$
- 二次因子 $(x^2+bx+c)^r$ ： $\frac{B_1x+C_1}{x^2+bx+c} + \cdots$

经典积分公式：

\int \frac{1}{(x+a)^k} dx = \begin{cases} \ln|x+a| + C & k=1 \\ \frac{(x+a)^{1-k}}{1-k} + C & k \geq 2 \end{cases}

2.2 三角替换

表达式形式	替换方式	参数范围
$\sqrt{a^2 - x^2}$	$x = a \sin t$	$t ∈ [-\pi/2, \pi/2]$
$\sqrt{x^2 - a^2}$	$x = a \sec t$	$t ∈ [0, \pi/2) ∪ (\pi, 3\pi/2]$
$a^2 + x^2$	$x = a \tan t$	$t ∈ (-\pi/2, \pi/2)$

例子：计算 $\int \frac{1}{\sqrt{a^2 - x^2}} dx$

解：令 $x = a \sin t$ ，则 $dx = a \cos t dt$

原式 $= \int \frac{a \cos t}{\sqrt{a^2 - a^2 \sin^2 t}} dt = \int dt = t + C = \arcsin(x/a) + C$

2.3 对数微分法

情形Ⅰ（乘积型）：

对 $y = f_1(x)f_2(x)\cdots f_n(x)$ ，取对数得：

\ln|y| = \sum_{i=1}^n \ln|f_i(x)| \\ \frac{y'}{y} = \sum_{i=1}^n \frac{f_i'(x)}{f_i(x)} \\ \Rightarrow y' = y \cdot \sum_{i=1}^n \frac{f_i'(x)}{f_i(x)}

例子：求 $y = x \sin x e^x$ 的导数

解： $\frac{y'}{y} = \frac{1}{x} + \cot x + 1 \Rightarrow y' = x \sin x e^x \left( \frac{1}{x} + \cot x + 1 \right)$

情形Ⅱ（幂指型）：

对 $y = f(x)^{g(x)}$ ，取对数得：

\ln y = g(x) \ln f(x) \\ \frac{y'}{y} = g'(x) \ln f(x) + g(x) \frac{f'(x)}{f(x)} \\ \Rightarrow y' = y \left[ g'(x) \ln f(x) + \frac{g(x)f'(x)}{f(x)} \right]

例子：求 $y = x^x$ 的导数

解： $\ln y = x \ln x \Rightarrow y' = x^x (\ln x + 1)$

三、特殊函数

3.1 自然对数函数

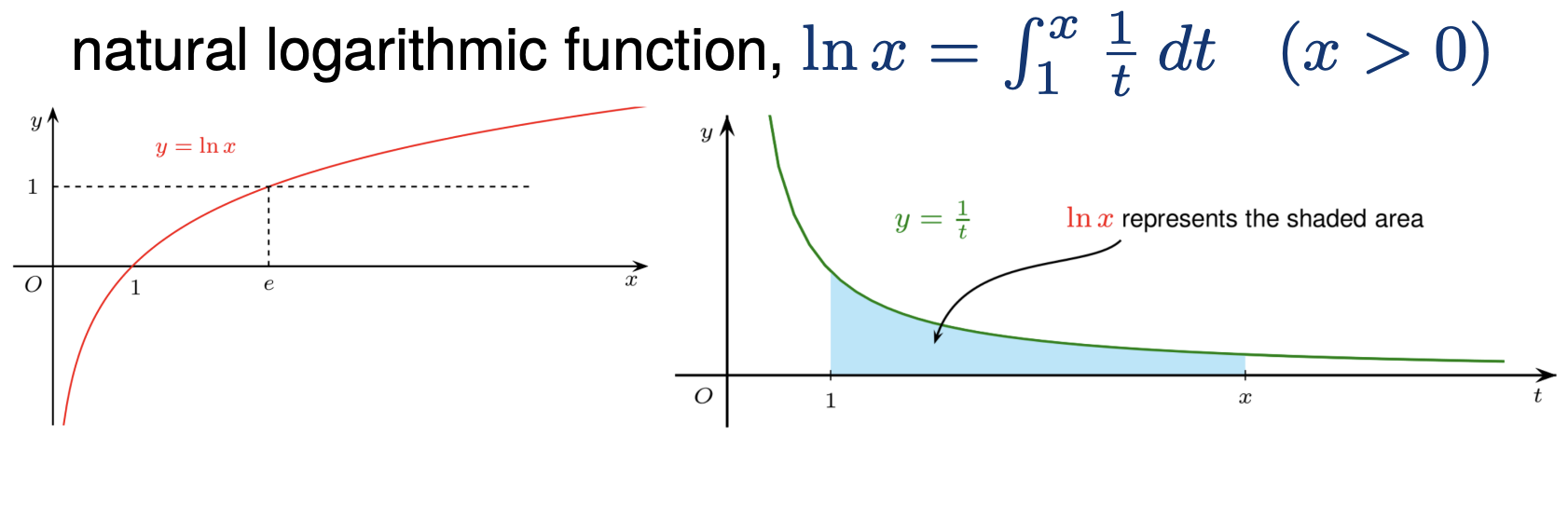
定义：

\ln x = \int_1^x \frac{1}{t} dt \quad (x > 0)

性质：

$\frac{d}{dx} \ln|x| = \frac{1}{x}$

$\ln 1 = 0$ , $\ln e = 1$ （其中 $e = \lim_{n→∞} (1+\frac{1}{n})^n$ ）

3.2 指数函数

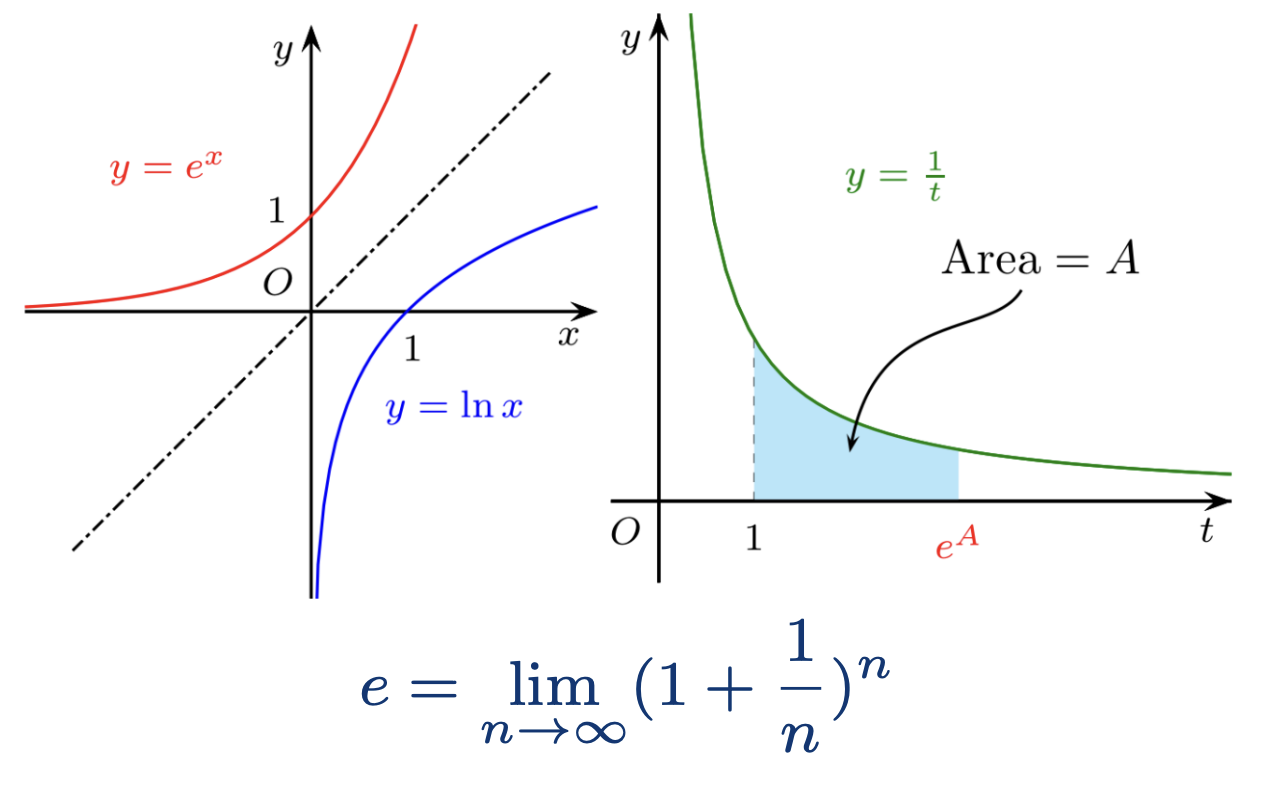
定义：

y = e^x \iff \ln y = x \\ a^x = e^{x \ln a}

重要极限：

\lim_{x→∞} \frac{e^x}{x^n} = ∞ \quad (\forall n ∈ \mathbb{Z}^+)

泰勒展开：

e^x = \sum_{n=0}^∞ \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots

3.3 双曲函数

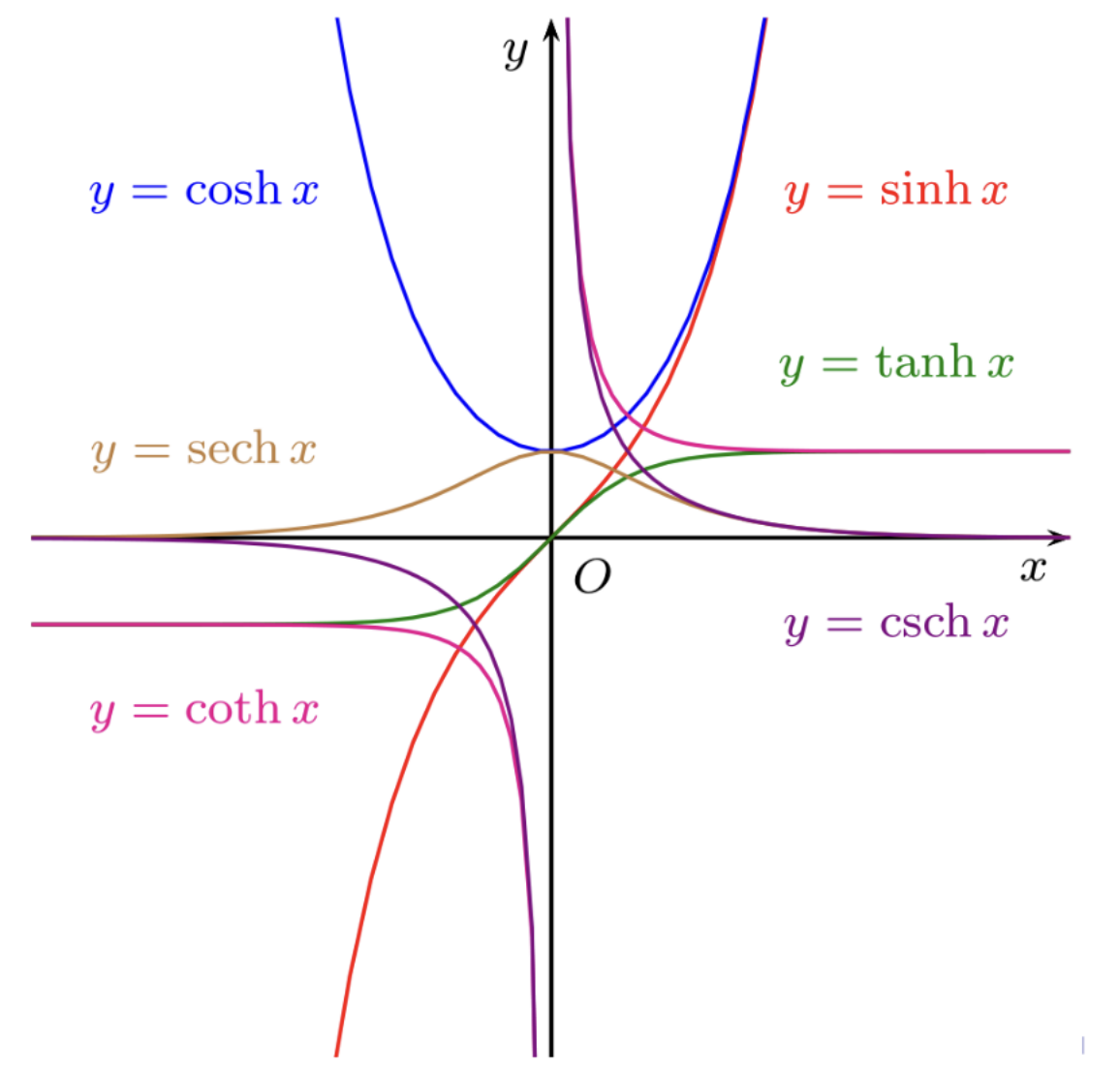
函数	定义式	导数
$\sinh x$	$\frac{e^x - e^{-x}}{2}$	$\cosh x$
$\cosh x$	$\frac{e^x + e^{-x}}{2}$	$\sinh x$
$\tanh x$	$\frac{\sinh x}{\cosh x}$	$\text{sech}^2 x$

恒等式：

\cosh^2 x - \sinh^2 x = 1

3.4 反双曲函数

函数	表达式	导数
$\sinh^{-1} x$	$\ln(x + \sqrt{x^2 + 1})$	$\frac{1}{\sqrt{x^2+1}}$
$\cosh^{-1} x$	$\ln(x + \sqrt{x^2 - 1})$	$\frac{1}{\sqrt{x^2-1}}$ (x > 1)
$\tanh^{-1} x$	$\frac{1}{2} \ln\frac{1+x}{1-x}$	$\frac{1}{1-x^2}$ (-1 < x < 1)

学习建议：

掌握反函数与导数的关系时，建议多画图理解几何意义

积分技巧需要大量练习，建议每天完成3-5道不同题型的积分题

对于特殊函数，记忆其定义式和图像特征更有利于应用

附：练习合集

练习

第6讲积分（Integrals）

第8讲积分应用（Appl. of Integrals）