第8讲 积分应用（Appl. of Integrals）

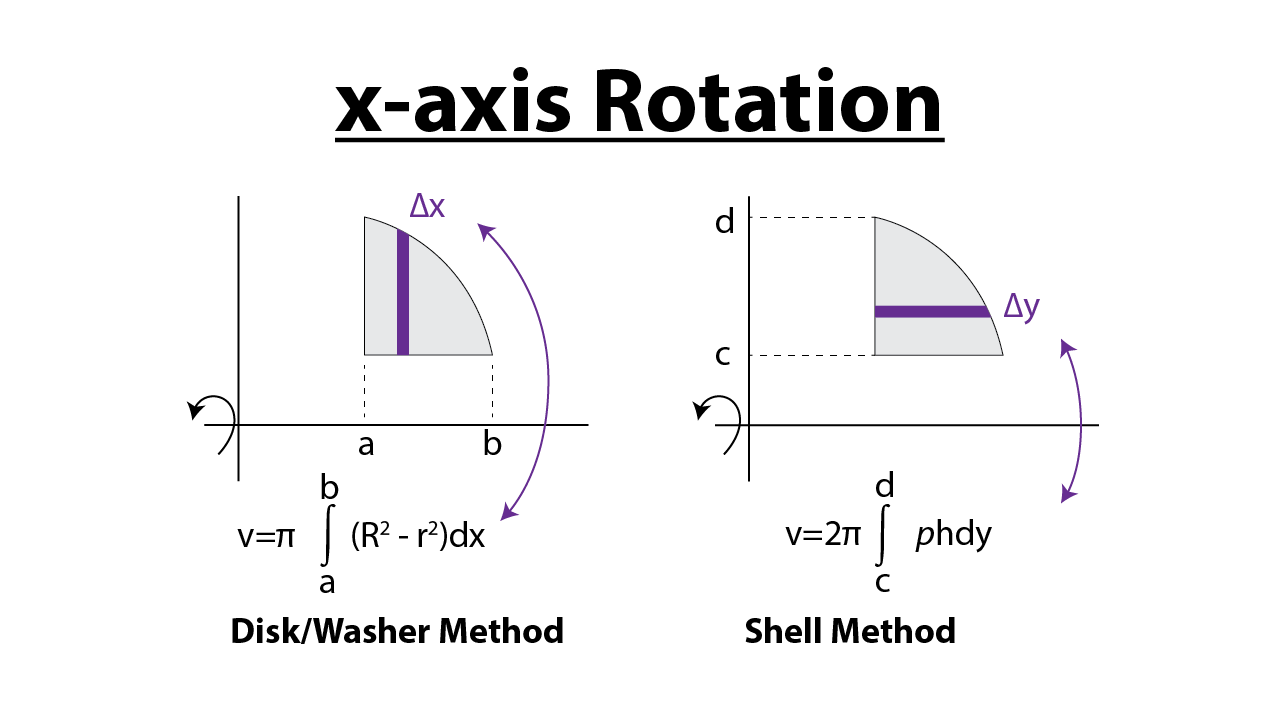
1. 旋转体体积/Volume of Revolution

1.1 圆盘/垫圈法 Disk/Washer Method

基本原理：将旋转体切割成无限薄的圆盘/垫圈，计算单个薄片体积后积分

绕x轴旋转（纵向切割）：

绕y轴旋转（横向切割）：

推导过程：

1. 在位置x处取厚度dx的薄片

2. 薄片半径r = f(x)

3. 单个薄片体积dV = πr²dx

4. 总体积为积分求和

示例：计算y = x²在[0,1]绕x轴的旋转体积

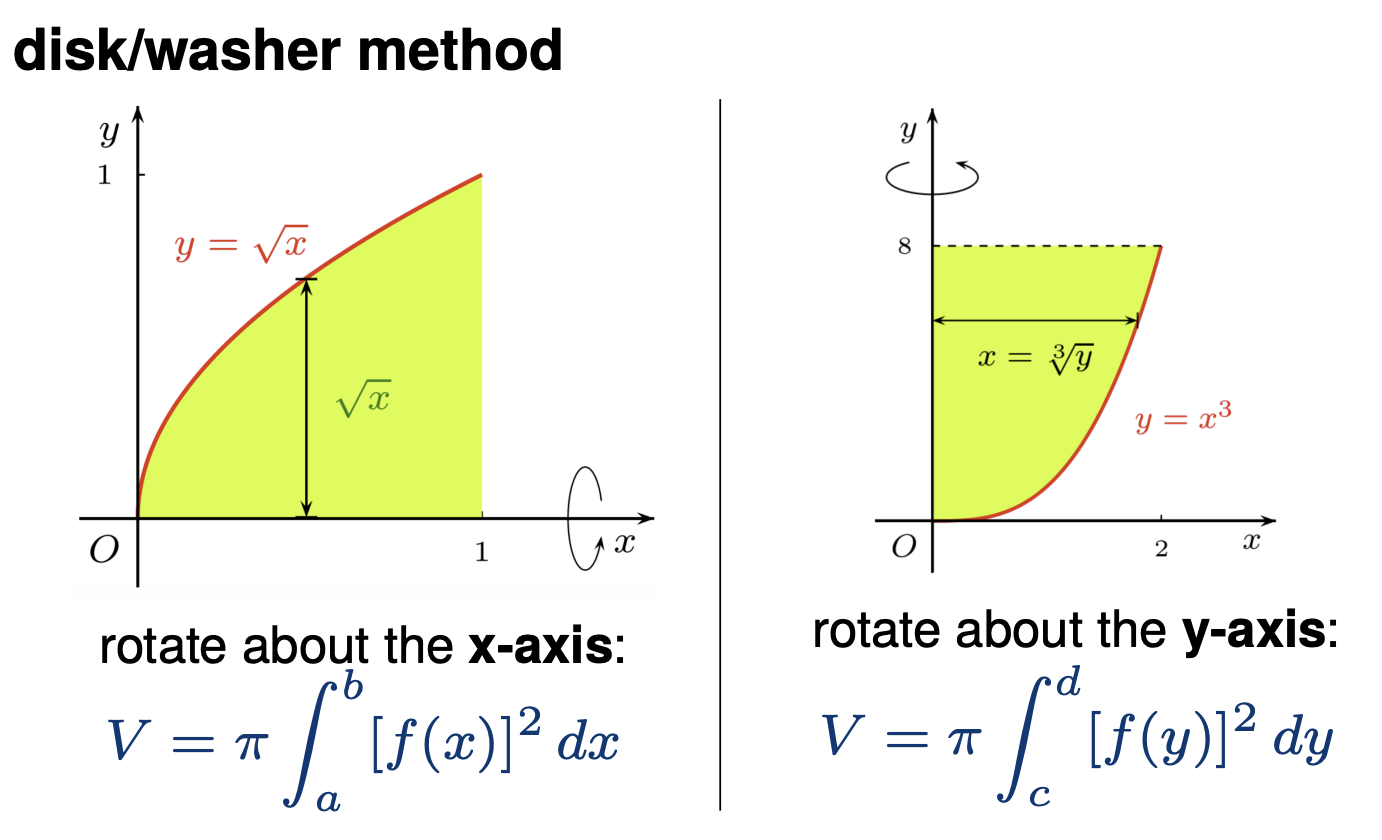
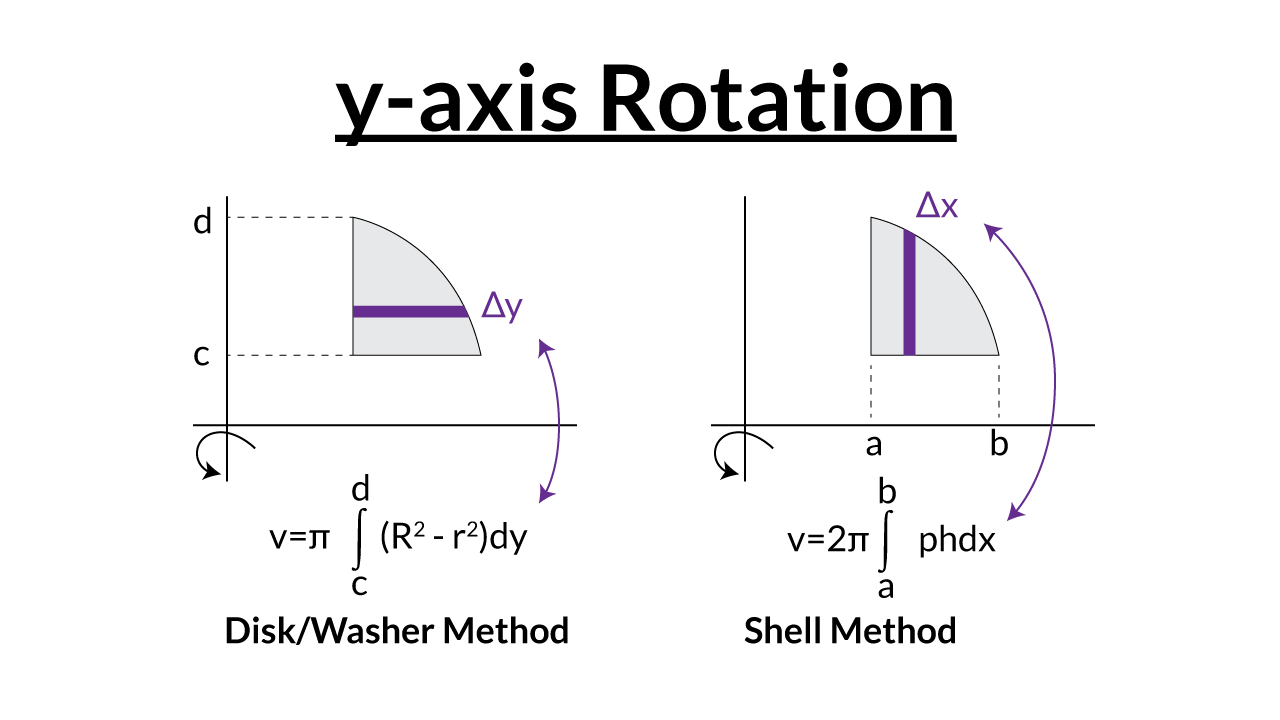
1.2 圆柱壳法 Cylindrical Shells Method

适用场景：当旋转轴与积分变量垂直时更简便

绕y轴旋转（垂直壳层）：

假设我们有一个曲线 y = f(x)，从 x = a 到 x = b。当这个区域绕y轴旋转时：

1. 取一个在 x 处的微小矩形，宽度为 dx，高度为 f(x)

2. 这个矩形绕y轴旋转后形成一个圆柱壳

3. 圆柱壳的半径就是 x（到y轴的距离）

4. 圆柱壳的高度是 f(x)

5. 圆柱壳的体积是：$dV = 2\pi \cdot 半径 \cdot 高度 \cdot 厚度 = 2\pi \cdot x \cdot f(x) \cdot dx$

6. 积分得到总体积：$V = 2\pi\int_{a}^{b} x \cdot f(x) dx$

绕x轴旋转（水平壳层）：

如果区域绕x轴旋转，我们可以用 y 作为变量，取曲线 $x = f^{-1}(y)$：

1. 每个圆柱壳的半径是 y（到x轴的距离）

2. 圆柱壳的高度是 $f^{-1}(y)$（水平距离）

3. 体积公式变为：$V = 2\pi\int_{c}^{d} y \cdot f^{-1}(y) dy$

示例：计算y = x在[0,1]绕y轴的旋转体积

学习建议：

1. 判断哪种方法更简便：看是否需要求反函数

2. 练习时建议先画示意图

3. 注意单位的一致性

1.3 对比Washer Method和Shell Method

在求解旋转体体积时，我们有两种主要方法：Washer Method（圆盘法，也称垫圈法）和Shell Method（圆柱壳法）。通过一个具体实例，我们可以比较这两种方法的应用：

考虑函数$y=x^2$和$x=\sqrt{y}$在矩形区域$[0,4]×[0,16]$内围成的区域。

1. 绕x轴旋转的体积

Washer Method：

当区域绕x轴旋转时，我们使用函数$y=x^2$在[0,4]区间内积分：

$V = \pi \int_0^4 (x^2)^2 dx = \pi \int_0^4 x^4 dx = \pi \left[ \frac{x^5}{5} \right]_0^4 = \frac{1024\pi}{5}$

Shell Method：

使用函数$x=\sqrt{y}$在[0,16]区间内积分：

$V = 2\pi \int_0^{16} y \cdot \sqrt{y} dy = 2\pi \int_0^{16} y^{3/2} dy = 2\pi \left[ \frac{y^{5/2}}{5/2} \right]_0^{16} = \frac{1024\pi}{5}$

2. 绕y轴旋转的体积

Washer Method：

当区域绕y轴旋转时，我们使用函数$x=\sqrt{y}$在[0,16]区间内积分：

$V = \pi \int_0^{16} (\sqrt{y})^2 dy = \pi \int_0^{16} y dy = \pi \left[ \frac{y^2}{2} \right]_0^{16} = 128\pi$

Shell Method：

使用函数$y=x^2$在[0,4]区间内积分：

$V = 2\pi \int_0^4 x \cdot x^2 dx = 2\pi \int_0^4 x^3 dx = 2\pi \left[ \frac{x^4}{4} \right]_0^4 = 128\pi$

方法比较：

1. 计算结果一致性：两种方法计算同一旋转体时得到相同的结果，这验证了计算的正确性。

2. 适用情境：
   • Washer Method适合当旋转轴与积分变量平行时使用
   • Shell Method适合当旋转轴与积分变量垂直时使用

3. 积分难度：在不同情境下，选择合适的方法可以简化积分过程。例如，在某些情况下，Shell Method可能导致更简单的积分表达式。

4. 几何直观性：
   • Washer Method考虑的是垂直于旋转轴的圆盘（或垫圈）
   • Shell Method考虑的是与旋转轴同心的圆柱壳

通过选择合适的方法，我们可以更高效地计算旋转体的体积

2. 曲线长度/Arc Length

2.1 基本公式

当函数f(x)在[a,b]上一阶导连续时，曲线长度计算公式：

参数方程形式：

示例：计算y = x²在[0,1]的弧长

$f'(x) = 2x$

$L = \int_{0}^{1} \sqrt{1 + (2x)^2} dx = \frac{1}{4}(2\sqrt{5} + \sinh^{-1}2)$

2.2 公式推导

1. 将曲线分割为n个微小直线段，每段长度记为$\Delta s_i$

2. 曲线总长度可以表示为：$L = \sum_{i=1}^{n} \Delta s_i$

3. 对于曲线y=f(x)上的相邻两点$(x_i,f(x_i))$和$(x_{i+1},f(x_{i+1}))$，该段直线长度为：

4. 当划分无限细化时，即$\Delta x_i \to 0$，可以得到微分弧长：

5. 根据微分中值定理，当$\Delta x_i$很小时，有$f(x_{i+1})-f(x_i) \approx f'(\xi_i)\Delta x_i$，其中$\xi_i \in [x_i,x_{i+1}]$，即$dy=f'(x)dx$

6. 代入并整理得：$ds = \sqrt{1 + [f'(x)]^2}dx$

7. 对整个区间积分得到曲线长度：$L = \int_{a}^{b} \sqrt{1 + [f'(x)]^2} dx$

参数方程情况：

当曲线由参数方程$x=x(t), y=y(t), t\in[t_1,t_2]$给出时：

1. $dx = \frac{dx}{dt}dt, dy = \frac{dy}{dt}dt$

2. 代入微分弧长公式：$ds = \sqrt{(dx)^2 + (dy)^2} = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2}dt$

3. 积分得到曲线长度：$L = \int_{t_1}^{t_2} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} dt$

3. 旋转体表面积/Surface Area of Revolution

绕x轴旋转的曲面面积：

推导要点：

1. 将曲线y=f(x)分割成微小段，每段长度为ds

2. 当绕x轴旋转时，每个微小弧段会形成一个微小的圆环带（近似圆台侧面）

3. 微小圆环带的面积：$dA = 2\pi r·ds$，其中r是到旋转轴的距离

4. 对于绕x轴旋转的情况，$r = f(x)$，即纵坐标值

5. 前面已推导出微分弧长：$ds = \sqrt{1 + [f'(x)]^2}dx$

6. 代入得到面积微元：$dA = 2\pi f(x)\sqrt{1 + [f'(x)]^2}dx$

7. 积分得到总面积：$A = \int_{a}^{b} 2\pi f(x)\sqrt{1 + [f'(x)]^2} dx$

绕y轴旋转时：

旋转曲面面积公式变为：$A = \int_{a}^{b} 2\pi x\sqrt{1 + [f'(x)]^2} dx$

参数方程形式：

当曲线由参数方程给出时，绕x轴旋转的面积为：

示例：计算y = x在[0,1]绕x轴的旋转表面积

$f(x) = x, f'(x) = 1$

$A = 2\pi\int_{0}^{1} x\sqrt{1 + 1} dx = 2\pi\sqrt{2}\int_{0}^{1} x dx = 2\pi\sqrt{2}·\frac{x^2}{2}\bigg|_{0}^{1} = \pi\sqrt{2}$

常见错误提醒：

1. 忘记乘以$2\pi$（旋转一周形成圆周）

2. 混淆弧长元素ds与微分dx（需正确使用$ds = \sqrt{1 + [f'(x)]^2}dx$）

3. 半径r取值错误（绕x轴旋转时r = f(x)；绕y轴旋转时r = x）

4. 积分区间设置错误（需与原曲线对应）

5. 当函数不是单值函数时，需分段计算

学习策略

1. 可视化优先：使用GeoGebra等工具观察旋转体形态

2. 维度分析：检查积分结果的量纲是否合理

3. 对比练习：同一问题尝试不同方法求解

4. 金融应用联想：虽然本节是几何应用，但积分技巧将在概率密度函数、期权定价模型等领域重现

附：练习合集