🦀
WQU Guru - MScFE
/
📄
Blog
/
📄
Quantopia-quantitative-analysis-56-lectures
/
第28讲：市场冲击模型 (Market Impact Models)
🔴
入学要求
💯
能力测试
🛣️
课程安排
🕹️
研究资源
🎑
博客
🔍
⋮
搭建于📝
🔴
入学要求
💯
能力测试
🛣️
课程安排
🕹️
研究资源
一、市场冲击和市场微观结构 1.1 市场冲击 1.2 市场微观结构 二、交易成本基础 2.1 交易成本的分类 2.2 价格滑点的影响因素 2.3 买卖价差和价格滑点的关系 三、流动性分析 3.1 日内流动性模式 3.2 订单执行时间估算 四、波动率分析 4.1 波动率的定义 4.2 历史波动率的计算方法 4.3 波动率的应用场景 五、市场冲击模型实践 5.1 Almgren-Chriss模型 5.2 其他模型 5.3 市场冲击模型的应用和局限性 实战练习 练习1：计算交易成本 练习2：流动性分析 优化建议 附：练习合集

第28讲：市场冲击模型 (Market Impact Models)

💡

查看全集：💎Quantopia量化分析56讲

一、市场冲击和市场微观结构

1.1 市场冲击

市场冲击（Market Impact）是指大宗交易行为对市场价格产生的影响。这种影响通常表现为：

市场冲击是交易成本的重要组成部分，尤其是对于机构投资者和量化交易者来说，理解和控制市场冲击至关重要。市场冲击由临时性冲击和永久性冲击共同构成：

临时性冲击

临时性冲击是由于交易执行时对市场流动性的暂时性压力所导致的价格变化。这种影响通常在交易完成后会逐渐消失。

公式：

ΔPtemp=α×(VVdaily)β\Delta P_{temp} = \alpha \times \left(\frac{V}{V_{daily}}\right)^{\beta}

其中：

这个公式表明，临时性冲击的大小与交易量相对于日均成交量的比例有关，并且这种关系是非线性的（由β决定）。

永久性冲击

永久性冲击是由于交易行为向市场传递了关于股票价值的信息，从而对市场价格产生持久的影响。其计算公式为：

ΔPperm=γ×QVdaily\Delta P_{perm} = \gamma \times \frac{Q}{V_{daily}}

其中：

这个公式说明，永久性冲击的大小与剩余待执行量成正比，并且受到市场对信息的敏感度（γ）的调节。

1.2 市场微观结构

标的资产基本状况

考察某流动性中等的股票，呈现以下市场特征：

流动性消耗分析

当市场参与者提交1000股市价买单(Market Buy Order)时，订单路由系统将按价格优先、时间优先原则执行如下操作：

  1. 第一层流动性消耗：立即匹配最优卖出价($100.05)的全部可用流动性，成交800股
  1. 流动性跃迁：由于一级卖盘流动性不足，剩余200股订单量将自动寻求第二层流动性
  1. 第二层匹配：与第二档卖盘(假设为$100.15)匹配剩余的200股
  1. 市场结构重构：交易完成后，订单簿重新整合，原第二档卖盘成为新的最优卖出价，价差扩大

执行成本分析

该市价单的实际执行价格为加权平均价：

(800股×$100.05+200股×$100.15)÷1000股=$100.07(800股 × \$100.05 + 200股 × \$100.15) ÷ 1000股 = \$100.07

该价格较原最新成交价高出7个基点，体现了流动性消耗对大额订单的价格影响，即所谓的市场冲击成本(Market Impact Cost)。

此案例展示了订单簿深度对交易执行质量的关键影响，也解释了为何机构投资者通常采用算法交易策略将大单拆分，以最小化市场冲击。

二、交易成本基础

2.1 交易成本的分类

直接成本：佣金和手续费（0.01%-0.05%）

# 示例：计算佣金（假设0.03%佣金率）
order_amount = 100000  # 10万美元订单
commission = order_amount * 0.0003
print(f"佣金成本：${commission:.2f}")

间接成本（关键分析对象）：

2.2 价格滑点的影响因素

价格滑点（Slippage）是指交易执行时，实际成交价格与预期价格之间的差异。预期价格通常是交易者下单时的市场报价或心中预期的价格。

因素影响机制典型值范围
波动率高波动性增加执行不确定性年化20%-50%
流动性低流动性导致价格冲击ADV 100万-5亿股
订单相对规模大订单更难隐蔽0.1%-5% ADV
买卖价差立即成交的显性成本5-50个基点 (bps)

1. 波动率

2. 流动性

3. 订单相对规模

4. 买卖价差

2.3 买卖价差和价格滑点的关系

示例对比：

概念定义主要影响因素性质
买卖价差买价和卖价之间的差额市场流动性、交易成本显性、静态成本
价格滑点实际成交价与预期价之间的差异买卖价差、市场波动、流动性、执行延迟隐性、动态成本

三、流动性分析

3.1 日内流动性模式

分析AAPL的日内交易量分布模式，下载2023年1月的苹果股票小时级数据，计算每个交易小时的平均成交量占比，并以柱状图形式展示：

import yfinance as yf
import matplotlib.pyplot as plt

# 获取苹果股票分钟级交易数据
aapl = yf.download('AAPL', start='2025-01-01', end='2025-01-31', interval='1h')
# 确保索引有时区信息（如果没有，假设为UTC）
if aapl.index.tzinfo is None:
    aapl.index = aapl.index.tz_localize('UTC')

# 将时间转换为美东时间
aapl.index = aapl.index.tz_convert('US/Eastern')

# 计算每小时成交量占比
hourly_volume = aapl.groupby(aapl.index.hour)['Volume'].mean()
hourly_pct = hourly_volume / hourly_volume.sum() * 100

# 使用pandas自带的绘图方法
ax = hourly_pct.plot(kind='bar', figsize=(10, 6), width=0.8)

# 设置图表属性
ax.set_title('AAPL Hourly Volume')
ax.set_xlabel('Trading Hour')
ax.set_ylabel('Volume')
ax.grid(axis='y')
plt.tight_layout()
plt.show()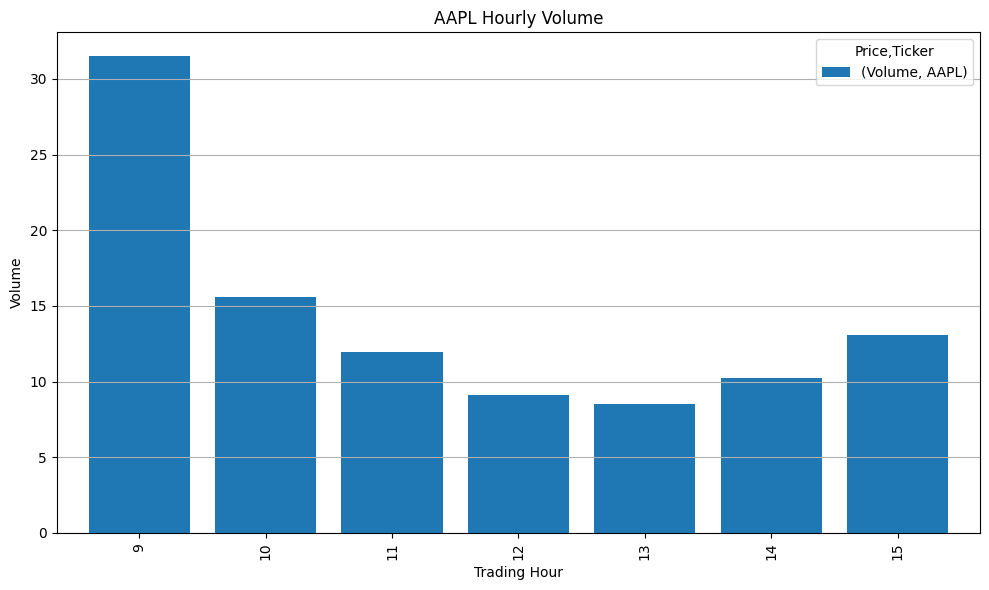

3.2 订单执行时间估算

核心公式是：

executionTime=orderSizeadv×participationRate×dailyTradingHoursexecutionTime = \frac{orderSize}{adv \times participationRate} \times dailyTradingHours

其中：

def estimate_execution_time(order_size, participation_rate, adv):
    """
    估算订单执行时间
    order_size: 订单量（股）
    participation_rate: 参与率（0-1）
    adv: 日均成交量（股）
    """
    daily_trading_hours = 6.5  # 美股每日交易时长（小时）
    interval_volume = adv * participation_rate
    return (order_size / interval_volume) * daily_trading_hours

# 示例：估算10万股订单执行时间
print(estimate_execution_time(1e5, 0.2, 1e6))  # 输出：3.25小时
参与率的影响因素：

四、波动率分析

4.1 波动率的定义

波动率（Volatility）是衡量资产价格变动幅度的统计指标，通常以资产收益率的标准差或方差来表示。它反映了资产价格的不确定性和风险水平：

波动率是量化市场行为的基础工具，广泛应用于金融分析中。根据计算方法和时间跨度的不同，波动率可以分为以下几种类型：

4.2 历史波动率的计算方法

历史波动率是基于资产历史价格数据计算得出的波动性指标。以下是几种常见的计算方法：

收盘价法（Close-to-Close Method）

收盘价法利用连续交易日的收盘价，计算对数收益率的标准差：

σclose=1N−1∑t=1N(rt−rˉ)2×252\sigma_{close} = \sqrt{\frac{1}{N-1}\sum_{t=1}^N (r_t - \bar{r})^2} \times \sqrt{252}

其中：

OHLC法（Garman-Klass）：

OHLC法综合利用开盘价（O）、最高价（H）、最低价（L）和收盘价（C）来估计波动率，捕捉日内价格波动信息：

σGK=1N∑t=1N[0.5(ln⁡Ht−ln⁡Lt)2−(2ln⁡2−1)(ln⁡Ct−ln⁡Ot)2]×252\sigma_{GK} = \sqrt{\frac{1}{N} \sum_{t=1}^N \left[ 0.5(\ln H_t - \ln L_t)^2 - (2\ln2-1)(\ln C_t - \ln O_t)^2 \right]} \times \sqrt{252}

其中：

公式各部分的含义

收盘价法和OHLC法例子：

def calculate_volatility(data, method='close'):
    if method == 'close':
        # 计算对数收益率
        returns = np.log(data['Close']/data['Close'].shift(1))
        std_dev = returns.std()
        # 等价于：
        # mean_return = returns.mean()  # 计算平均收益率 \bar{r}
				# std_dev = np.sqrt(((returns - mean_return)**2).sum() / (len(returns) - 1))
        return std_dev * np.sqrt(252)
    elif method == 'garman-klass':
        log_hl = np.log(data['High']/data['Low'])
        log_co = np.log(data['Close']/data['Open'])
        daily_var = 0.5*log_hl**2 - (2*np.log(2)-1)*log_co**2
        return np.sqrt(daily_var.mean() * 252)

其他方法

4.3 波动率的应用场景

波动率在金融领域有多种实际用途：

尽管波动率是一个强大的分析工具，但其应用也存在一些限制：

五、市场冲击模型实践

市场冲击模型有多种变体，适用于不同的交易场景。以下是对几种常见模型的对比分析：

模型核心变量适用场景特点与优势
Almgren-Chriss波动率、订单规模、执行时间中低频策略、大额订单执行强调交易速度与冲击的非线性关系，适合流动性好的市场。
KissellPOV（参与率）高频做市策略、快速执行基于参与率（Percentage of Volume），适合高频交易。
JPM 模型买卖价差、流动性大额订单执行、流动性不足市场考虑市场深度和买卖价差，适用于低流动性资产。
Quantopian成交量占比平方小规模快速交易、算法交易简单易用，假设冲击与成交量占比平方成正比。

补充说明：

5.1 Almgren-Chriss模型

Almgren-Chriss 模型是量化交易中广泛使用的市场冲击模型，通过将市场冲击分为永久性冲击和暂时性冲击两部分，帮助交易者评估和优化交易成本。

永久性冲击

永久性冲击（Permanent Impact）反映交易行为对市场价格的长期影响，通常与交易量和市场流动性相关。其计算公式为：

Iperm=γσXVI_{perm} = \gamma \sigma \sqrt{\frac{X}{V}}

其中：

解读：

暂时性冲击

暂时性冲击（Temporary Impact）反映交易行为对市场价格的短期影响，通常在交易完成后逐渐消散。其计算公式为：

Itemp=ησ(XVT)3/5I_{temp} = \eta \sigma \left( \frac{X}{VT} \right)^{3/5}

其中：

解读：

以下是一个简单的 Almgren-Chriss 模型实现，用于计算市场冲击成本（以基点 bps 为单位）：

import numpy as np

def almgren_impact(order_pct_adv, annual_vol, days=1):
    """
    计算 Almgren-Chriss 模型的市场冲击成本
    参数：
        order_pct_adv: 订单占日均成交量（ADV）的比例（例如 0.05 表示 5%）
        annual_vol: 年化波动率（小数形式，例如 0.25 表示 25%）
        days: 执行天数（默认 1 天）
    返回：
        市场冲击成本（单位：bps）
    """
    gamma = 0.314  # 永久性冲击系数
    eta = 0.142    # 暂时性冲击系数

    permanent = gamma * annual_vol * np.sqrt(order_pct_adv)
    temporary = eta * annual_vol * (order_pct_adv / days) ** 0.6
    total_impact = (permanent + temporary) * 10000  # 转换为 bps
    return total_impact

# 示例计算
impact = almgren_impact(0.05, 0.25, 1)
print(f"市场冲击成本：{impact:.2f} bps")

示例输出：假设订单占 ADV 的 5%（0.05），年化波动率 25%（0.25），执行时间 1 天，市场冲击成本约为 34.56 bps。

应用场景

5.2 其他模型

Kissell模型

Kissell模型关注交易的参与率（Percentage of Volume, POV），即交易量占市场总成交量的比例：

该模型适用于高频交易和做市策略，能够根据市场情况实时调整交易速度。

JPM模型

JPM模型（摩根大通模型）考虑市场深度和买卖价差，特别适用于低流动性资产：

该模型在大额订单和流动性不足的市场中表现较好。

Quantopian模型

Quantopian模型是一种简化的市场冲击模型，假设冲击与交易量占比的平方成正比：

该模型计算简单，适合小规模快速交易，但在复杂市场条件下表现有限。

5.3 市场冲击模型的应用和局限性

市场冲击模型在量化交易中具有广泛的应用：

尽管市场冲击模型非常重要，但也存在一些局限性：

实战练习

练习1：计算交易成本

假设某股票：

使用Almgren模型计算预期交易成本（bps和美元）

order_size = 50000
adv = 1e6
price = 150
annual_vol = 0.3
hours = 2

order_pct = order_size / adv
days = hours / 6.5

cost_bps = almgren_impact(order_pct, annual_vol, days)
cost_dollar = (cost_bps / 10000) * order_size * price

print(f"预期成本：{cost_bps:.2f} bps")
print(f"美元成本：${cost_dollar:.2f}")

练习2：流动性分析

使用yfinance获取TSLA最近一个月的交易数据：

  1. 绘制日内成交量分布图
  1. 计算不同时段的平均买卖价差
  1. 估算10万股订单在不同参与率下的执行时间
# 获取TSLA数据
tsla = yf.download('TSLA', period='1mo', interval='1h')

# 计算买卖价差
tsla['Spread'] = (tsla['Ask'] - tsla['Bid']) / tsla['Ask'] * 10000  # bps

# 按小时分析
hourly_spread = tsla.groupby(tsla.index.hour)['Spread'].mean()

plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
tsla.groupby(tsla.index.hour)['Volume'].mean().plot(kind='bar')
plt.title('TSLA日内成交量分布')

plt.subplot(1,2,2)
hourly_spread.plot(kind='bar', color='orange')
plt.title('TSLA日内平均价差 (bps)')
plt.tight_layout()
plt.show()

优化建议

  1. 订单拆分：大额订单分拆为多个小额订单
  1. 流动性择时：选择高流动性时段交易
  1. 算法选择：
    • VWAP：流动性平均分布时
    • TWAP：需要稳定执行节奏
    • Implementation Shortfall：平衡价格风险与冲击成本
  1. 监控指标：
    • 实际成交价与到达价的偏差
    • 订单完成率
    • 市场冲击成本占比

通过本教程，您已经掌握了市场冲击分析的核心概念和实践方法。建议在实际交易中持续监测执行质量，并建立自己的成本数据库以优化交易策略。

附：练习合集

练习